29度台形ねじ 山の頂及び谷底の切取りが大きい対称断面形のねじをもち、ねじの各部の寸法を 1 mm 基準として決めた、ねじ山の角度が 29°の台形ねじ。 29degree trapezoidal screw thread 1313 角ねじ(かくねじ) ねじ山の断面形が正方形に近いねじ。台形の面積の公式 台形の面積は 『(上底下底)×高さ÷2 ÷ 2 』 で求めることができます。 たとえば以下のような問題の場合。 例題 上底3cm、下底7cm、高さ6cmの台形の面積を求めよ。 答えはこのように求めることができます。 (3 7)× 6÷2=30(cm2) ( 3 7) ×17/5/12 台形の定義:向かい合う辺のうち、少なくとも1つが平行であるような四角形 >あと三角形の定義、定理についても >定義 三辺が同じ
2
台形 角度 定義
台形 角度 定義-台形の性質 台形の性質 四角形のうちで、一組の対辺が平行なものが台形である。 台形の面積 S の公式として次が知られている。 『 (上底+下底)×高さ÷2 』と、そらんじておられ る方も多いだろう。 教科書等では、通常、次のような形で説明されている。 同じ台形を2つ用意し、下図のように組み合わせて平行四辺形を作る。 平行四辺形の面積の公式から台形・平行四辺形・ひし形・対角線とは(1) 名前 台形 平行四辺形 ひし形 平行四辺形 長方形 ひし形 正方形 1次 の(1 )2 ようなせいし つ を持 四角形 、次 ア~オ 中からすべて選び記号 で答えなさい。



棱台怎么做 万图壁纸网
BASICα、等脚台形、補助線 BASIC α このページは公立中学校の2年までに習う内 容を基本とし、それとプラスアルファの内容で この「スウガクとくガウス」は事足りるかな~ いうわけで、チュートリアルみたいなもんです。 対頂角 ∠x = ∠y 同位外角(がいかく)とは、多角形の外側にできる角です。 一方、多角形の内部にできる角を「内角(ないかく)」といいます。 三角形の場合、内角の和は180度になります。 今回は外角の意味、求め方、内角との違い、外角と内角の和について説明します。 内角の和、内角の意味は下記が参考になります。 内角の和と三角形の関係は? 1分でわかる和の値、証明台形の面積=(上底下底)×高さ÷2ですね。 平行な2つの辺のうち、どちらを上底、下底としてもよいので、 4と6が入れかわっていても間違いではありません。 ただし、学校によっては決められた順番どおりに式を書いていないと 減点する場合があります。 学校では、学校の先生の指導にしたがってください。
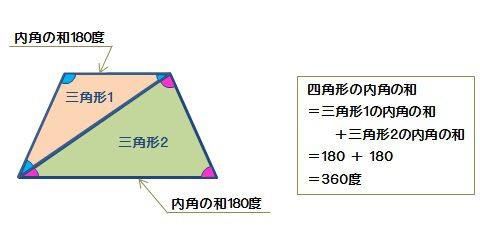
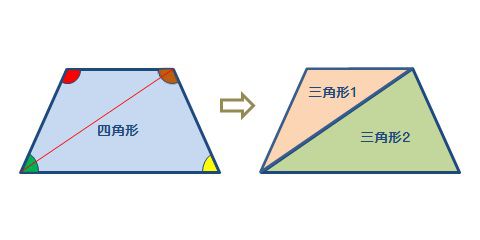
図形の定義及び性質〔参考:算数教科書の定義・定理辞典 著 志水廣 啓林館わくわく算数〕 図形 定義 性質 三角形 3本の直線で囲まれた図形 角が3つある。 角の総和は180°である。 四角形 4本の直線で囲まれた図形 角が4つある。台形の底辺と面積は下式の関係があります。 A=(ab)h/2 Aは台形の面積、aは台形の上底、bは台形の下底、hは台形の高さです。下図をみてください。 なぜ、台形の底辺と面積が上式の関係になるか示します。まず台形に対角線を引いてください。タイミングベルト(台形歯)資料〈1〉 ―G‐― タイミングベルト 資料〈1〉 許容最小プーリ径と歯数表 軸間距離の調整代 内側調整代 ベルト巾とプーリ巾の関係 ベルト巾公差 ベルト形別 回転数 rpm ピッチ径 mm歯数 575 690 870 1160 1750 3500 6000
19/2/ 台形の計算問題 計算問題①「台形の面積と角度を求める」 計算問題②「台形の高さを求める」 計算問題③「台形の面積比から辺の比を求める」 台形とは? 定義 台形とは、 少なくとも 組の向かい合う辺がお互いに平行であるような四角形 のことをいいます。 平行な 本の向かい合う辺を台形の 底辺 といい、そのうち一方を 上底 、もう一方を 下底 等脚台形(とうきゃくだいけい、米語: isosceles trapezoid, 英語: isosceles trapezium )は、台形の一種で、1本の底辺の両端の内角が互いに等しい図形である。このとき、もう一組の底辺の両端の内角も互いに等しくなる。定義を十分に理解さ せるためには,角の測定や作図をていねいに取り扱う必要がある。 台形と平行四辺形,ひし形の意味と作図では,まず辺の平行関係に着目して四角形を仲間分け する活動を通して,台形,平行四辺形,ひし形を定義する。




Lang Comp Pdf



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
平行線の定義・・・錯角の等しい2直線は平行である。 この定義から次の性質、条件が導ける。 平行線の性質 2つの直線に1つの直線が交わるとき、 2つの直線が 平行なら錯角は等しい 。 2つの直線が 平行なら同位角は等しい 。 平行線になる条件25/8/21 第1章 7.「図形」領域における教科書記述の研究 「図形」領域における教科書記述の研究として実施した、ワーキンググループの報告内容は以下の通りである。 図形ワーキンググループで、図形の分野において議論ならびに検討された内容について整理し台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から)



梯形




18 0012号 下向き溶接における溶接条件作成方法 Astamuse
二等辺三角形の選択した2つの入力値から他の要素の値を計算します 使用目的 スピーカーの設置 ご意見・ご感想 音楽鑑賞において、スピーカーと自分を点で結んだ際に正三角形になるのが良いとされているが、自分にとって最適な角度を見つけたかったので、この計算サイトはとても役に本 形の定義を理解 形をつくる。 いろいろな四角形を弁 時 する。 ・四角形の仲間分けをする。 別しようとしている。 ・「台形」と「平行四辺形」の定義を 知台形,平行四辺形の定 知る。 義を理解して 解説&答えはこちら 答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく




小5 算数 小5 32 四角形の角度 Youtube
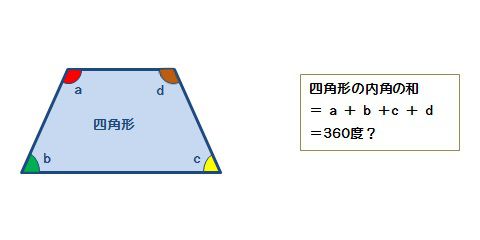
長方形や正方形は全ての角度が90度ですから、 それが4個あるので 90度×4=360度 となります とても簡単ですよね? しかし これだと面白くないので少し違う考え方をします 下の図は台形ですが、 この四角形の内角の和を 台形とは?定義や公式(面積の求め方)、性質、面積比の計算問題などQ台形ねじ技術計算 1接触面圧P、2すべり速度V算出 pv 値グラフより p、v の交点が内側にあるか確認 使用条件の決定 軸方向荷重、回転数 台形ねじナット型式の仮決定 台形ねじナット材質 3ねじ効率η、4負荷トルクt の算出 モータ等の選定に使用 ngブリタニカ国際大百科事典 小項目事典 台形の用語解説 梯形 (ていけい) ともいう。四辺形のそれぞれの対辺を a ,b と c ,d とし,a ,b は互いに平行で,c ,d が互いに平行でないものをいう。この場合,a ,b を台形の底といい,c ,d を台形の脚という。



形变观测数据的多异常形态统一识别



学术 K波段圆波导天线及阵列设计 微波eda网
定義2つの辺が等しい三角形 四角形は、平行四辺形 2組の対角がそれぞれ等しい 二等辺三角形の 底角は等しい 対角線がそれぞれの中点で 交わる四角形は、平行四辺形 二等辺三角形の頂角の二等分線は, 底辺を垂直に2 等分する さが等しい25/1/18 この台形の中から相似な三角形を探していくと 対頂角や錯角が等しくなることから OADと OCBが相似になることがわかります。 台形(だいけい、米 trapezoid 、英 trapezium )は、四角形の一部で、少なくとも一組の対辺が互いに平行であるような図形である。平行な2本の対辺を台形の底辺といい、そのうち一方を上底(じょうてい)、他方を下底(かてい)とよぶ。




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



不容错过的房间风水布局风水常识大有学问
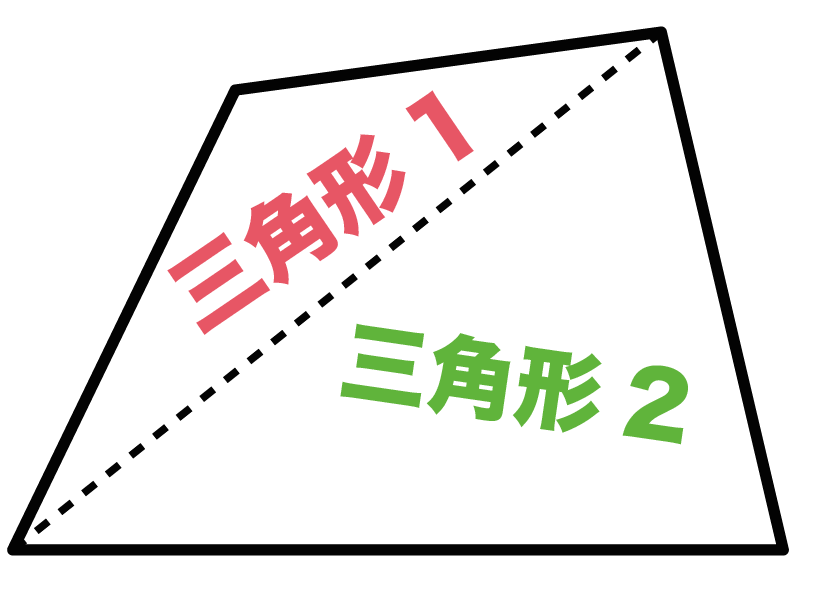
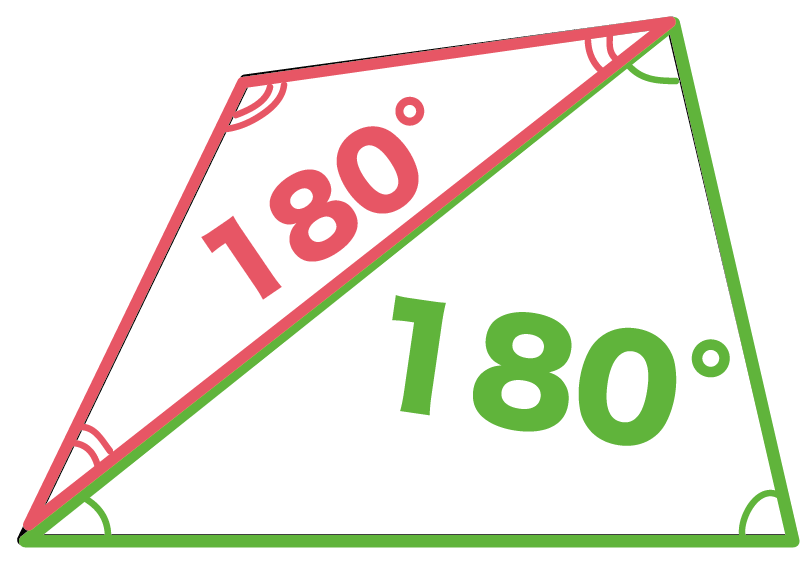
台形 四角形の4本の辺のうち、2本が平行になっている 図形を台形といいます。このとき右の図1のよう に台形では 角A+角B=180(度) 角C+角D=180(度)になっています。 図2、図3、図4のいずれも台形ですが、台形の面積は、ご存じの通り(上底+下底)×高さ÷2で求められる。 これをかつては小学校の5年生で教え込まれた。 しかし、この「公式」は、小学校時代のテストで使う以外に、ほとんど使用用途がない。 小学校の算数は、中学、高校の数学につながっ作成中中学受験台形の特徴と性質とは?基本 台形の角度 ルール 四角形は三角形を2つ含んでいるので、内角の合計は180×2=360度になります。台形も同様です ((図)) さらに、上底と下底が平行なので、平行線が作る角度が使えます。



Http Www Kochinet Ed Jp Kawanobori E Kounaikennkyuu 5 6nenn6 22 Pdf



形变观测数据的多异常形态统一识别
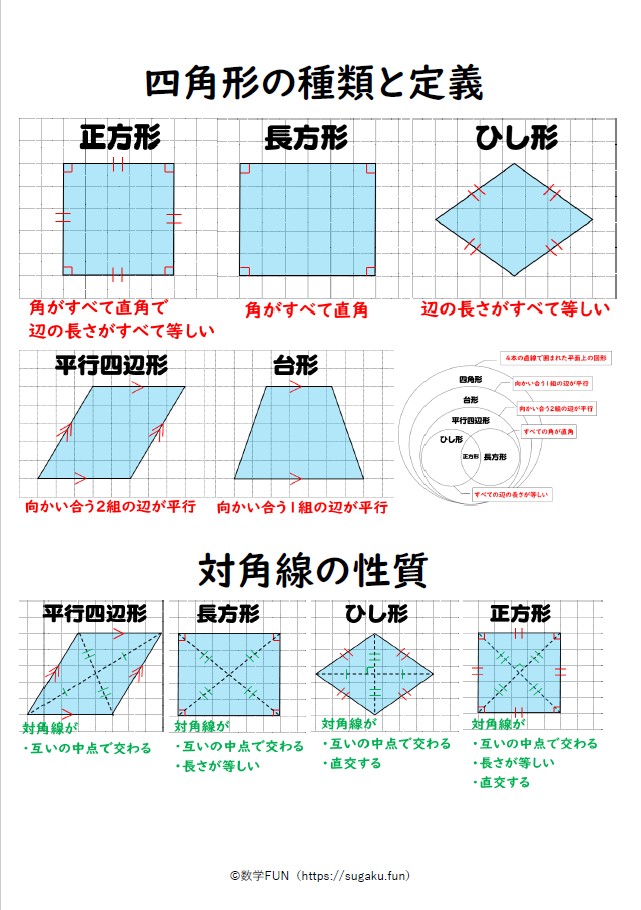
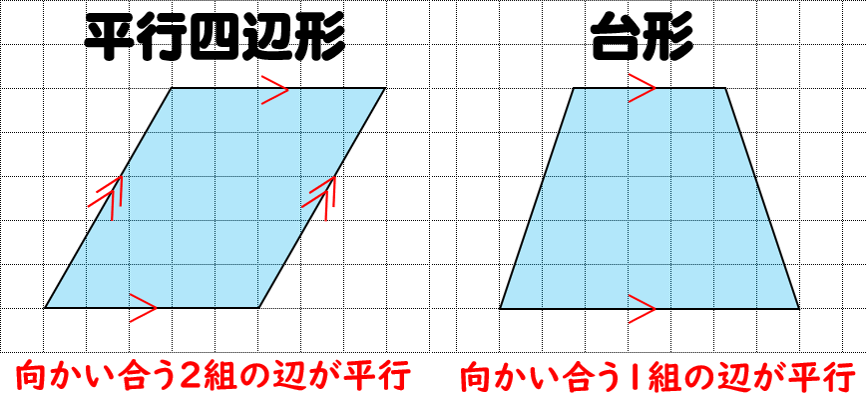
台形,平行四辺形,ひし形について理解し,図形についての見方や感覚を豊かにする。 関 身の回りから垂直な2 直線や平行な2 直線及び,台形,平行四辺形,ひし形などを見つけ,それ らが使われる場面について考えようとしている。 考長方形や正方形は全ての角度が90度ですから、 それが4個あるので 90度×4=360度 となります。とても簡単ですよね? しかし これだと面白くないので少し違う考え方をします。 下の図は台形ですが、 この四角形の内角の和を求めていきましょう。平行四辺形: 向かい合う2組の辺が平行な四角形 台形: 向かい合う1組の辺が平行な四角形 注意点として、 "長方形" や "ひし形" も向かい合う辺は平行なので 『平行四辺形の定義』 に当てはまりますし、 "正方形" は 『長方形・ひし形の定義』 にも当てはまります。 つまり どんな"正方形"も"長方形"であり、"ひし形"でもあり、"平行四辺形"でも



19uabb深双 城市之眼 板块导览 建日筑闻 微信公众号文章阅读 Wemp



独立基础柱墩图片 图片欣赏中心 急不急图文 Jpjww Com



与君歌 比观众开上帝视角吐槽 更可怕的是演员的演技 娱乐资讯 娱乐新闻网



ラングレーの問題 整角四角形



Http Www Mitsubishielectric Com Fa Assist Fa Dictionary Pdf Lgera Pdf



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




Jpa Method For Working Surface Of Aluminum Plate Base Material For Lithographic Printing Plate And Lithographic Printing Plate Google Patents




台形の対角線の求め方 この図のaとcの対角線の求め方を教えて下さい 数学 教えて Goo



同 界 角 定義



鲁里纳刻 Mundolatas




等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




Pdf Structure Optimization Of Concentrating Solar Thermal Cavity Receiver



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく




Opengl系列 2 设置可视空间 野生猿 群号 Csdn博客



15 Solidworks 定义修正梯形剖面



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



圆台下料展开计算方法 冲压模具设计篇 钣金件产品展开计算与画法 值得收藏学习 邬盛的博客 程序员宅基地




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



嘉行新悦李妍 以内部自循环孵化有辨识度的偶像 新偶像系列报道 体育头条



Http Www Smvhs Kh Edu Tw Ezfiles 1 1001 Attach 19 Pta 527 Pdf



2



中国舰船研究



等脚台形の性質って何ですか 一組の対辺が平行 かつ 別のも Yahoo 知恵袋



年下半年 7月25日 四川省公务员考试行测真题及答案解析 行测真题 高教公考试题库




Woa1 Connection Structure For Superconducting Cable Google Patents



新 观点 国土空间规划视角下的文化遗产空间体系建构 认知
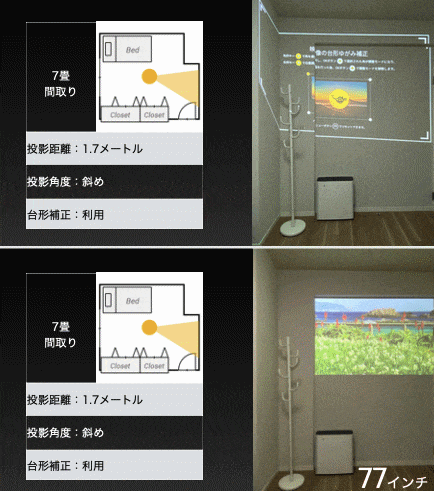



极米科技popin Aladdin 2正式发布 手机新浪网




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



圆台下料展开计算方法 冲压模具设计篇 钣金件产品展开计算与画法 值得收藏学习 邬盛的博客 程序员宅基地




剪力墙结构模板施工专项方案 精确计算 文库吧



添付した図のような台形の xの角度を求めようと思っています 参 Yahoo 知恵袋



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



倾斜角度射击与玻璃破碎痕迹分析




實木家具榫頭及榫槽的加工方法 每日頭條




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



考虑细长杆件不同坠落角度的海洋平台甲板损伤预报方法



圆周运动 图片欣赏中心 急不急图文 Jpjww Com



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



国土空间规划视角下的文化遗产空间体系建构 认知



コンプリート 多角形角度公式 ニスヌーピー壁紙




Space 62 Exhibition By George Lam Issuu
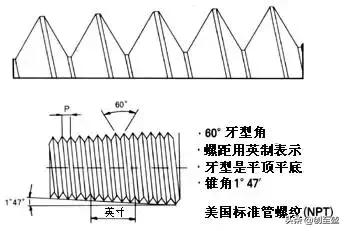



Unef螺纹 Pt螺纹 Npt螺纹 G螺纹 公制螺纹的区别 随光追影的博客 程序员宅基地 程序员宅基地
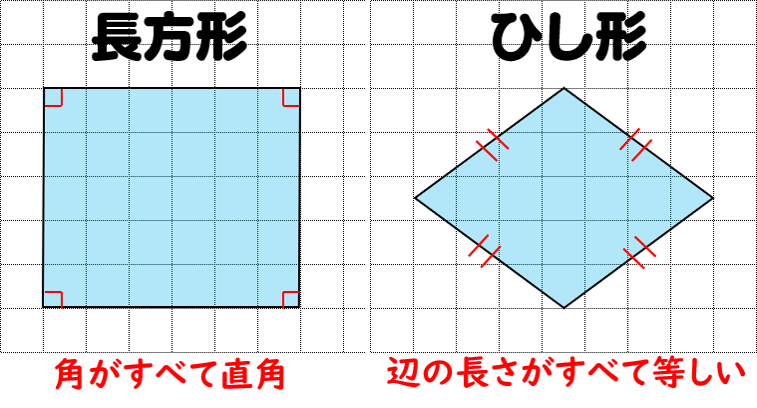



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




極米科技刷爆日本 朋友圈 Popin Aladdin 2正式發佈 每日頭條



倾斜角度射击与玻璃破碎痕迹分析




含稅價 型號 工具先生 日本鶴龜shinwa 企鵝 角尺45度90度台形止型定規 露天拍賣



小4算数の宿題です の角度を分度器を使わずに求める問題です Yahoo 知恵袋



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
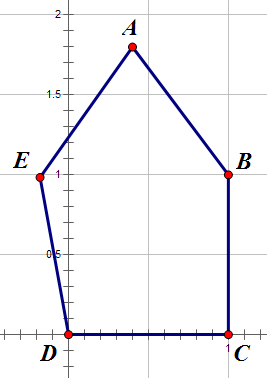



正五边形各角度数 正五边形的角是多 五边形的角度是多少



コンプリート 多角形角度公式 ニスヌーピー壁紙



形变观测数据的多异常形态统一识别




Cnu 磨削工具 Google Patents




Woa1 Surface Microstructure Measuring Method Surface Microstructure Measurement Data Analyzing Method And X Ray Scattering Measuring Device Google Patents



角度を教えてください 台形は 四角形の一部で 少なくとも Yahoo 知恵袋




Woa1 Connection Structure For Superconducting Cable Google Patents




台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



2



不同类型偏差对激光聚焦系统聚焦性能的影响



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



Happyripple的微博 微博
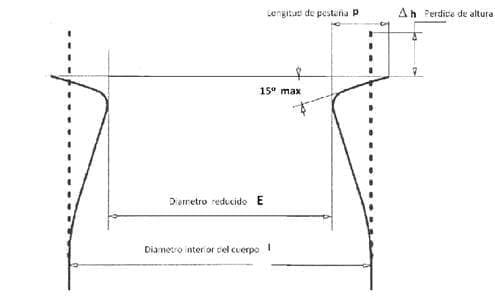



鲁里纳刻 Mundolatas



公司业绩 吉林省吉泰安全技术服务有限公司



投影机常见的两种类型投影机原理



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



R 角 定義




コノエ台形ネジ s45c 左ねじ tr50x1210 品番 Ntrl 0 送料別途見積り 法人 事業所限定 掲外取寄 ホームセンターバロー店コノエその他締結部品



棱台怎么做 万图壁纸网



等脚台形の条件を教えてください 台形の定義は 1組の向かい合う辺が Yahoo 知恵袋



倾斜角度射击与玻璃破碎痕迹分析




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



2




等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張



四角形の内角の和 算数の公式覚えてますか



形变观测数据的多异常形态统一识别



Basic A 等脚台形 補助線




台形と平行四辺形の定義 ちがい 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



四角形の内角の和 算数の公式覚えてますか



四角形の内角の和 算数の公式覚えてますか



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




数学 台形 角度の問題教えて 添付の台形 Dの角度が1 になる理由 数学 教えて Goo




当众表演 强暴 戏被质疑不尊重女演员 我是女演员 总监制独家回应 考虑欠缺 已从正片删除 惠英红 郑元畅 网易新闻




Cnu 磨削工具 Google Patents




台形と平行四辺形の定義 ちがい 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




複雜基礎的鋼筋如何布置第二講 壹讀



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



0 件のコメント:
コメントを投稿