√ 方程式 の やり方 298478

 こんにちは。 da Vinch (@mathsouko_vinch)です。 解を簡単に求められない場合の不定方程式の解き方その1では「一つでも解が求められれば不定方程式は解ける」と学びました。今回はその一つがなかなか見つけられないときにど式の中にある値を代入すると成り立つ等式を方程式という。 また、方程式を成り立たせる値を 解 といい、方程式の解をもとめることを 「方程式を解く」 という。 例 方程式　3x 1 = x 5について中2数学連立方程式の代入法の解き方について解説！ 中学生の勉強方法 115 中2数学文字を含んだ図形の体積の求め方とは？単項式の計算を解説！ 中学生の勉強方法 714 中1数学立体図形円柱と円錐、球について学ぼう！

徹底解説 連立方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

方程式 の やり方

方程式 の やり方-二次方程式に解を与える最初期の方法は幾何学的であった。バビロニアの楔形文字で書かれた文字板には二次方程式を解くことに単純化可能な問題が含まれていた エジプト中王国の時代（紀元前50年 紀元前1650年）にまで遡る、エジプトの ベルリンパピルス （英語版） には二項の二次方程式さて、ここまで来れば方程式の計算マスターまであと一歩です。 例5 次の方程式を解きなさい。 小数の項が両辺にある場合は、両辺に10や100をかけて、すべての項を整数にしてから計算します。 また、両辺に分数がある場合は、分母の最小公倍数を

3

ドレイクの方程式（ドレイクのほうていしき、英語 Drake equation ）とは、我々の銀河系に存在し人類とコンタクトする可能性のある地球外文明の数を推定する算術的な式である。 「方程式」と通例として呼ばれてはいるが、代数方程式などのような、いわゆる方程式ではない。 やり方の①を 少し細かく見ます 分数のままでも 方程式を解くことはできます しかし、 ミスが多くなるので まず、「分数の式」を 「整数だけの式」にします 「分母をはらう」といいますPocket 今回の記事では、中1で学習する一次方程式の解き方についてまとめていくよ！ 基本的な方程式の解き方から分数、小数を含む方程式の解き方まで説明していきます。 分数、小数が出てくると難しく思えちゃうんだけど、ある手順をしっかりと踏めば

 方程式の問題の解き方（2）：逆数をかける （例）方程式 2 x = 6 を解いてください これも方程式を解いてください、じゃから、「x ＝ 」の形を目指すわけじゃな 数学おじさん そのためには、 まず、問題の式と、目的の式をよーく見比べてみてほしいん semのやり方 改訂版 1 semのやり方 2 因子分析→構造方程式モデルにチェック 準備 3 使う変数を全部投入 左から独立変数、（媒介変数、）従属変数に したほうが後々便利 独 立 媒 介 従 属 従 属 4 モデルスペースを選択 5 方程式の解き方かっこがあるときのまとめ 理解したよ！ やり方をしっかりと覚えておこう！ まず、方程式のかっこをはずす。 そして、いつも通り解くだけ！ たったこれだけのことです。 だけど、やっぱりね 普通の方程式よりも計算力は必要

1つの方程式の両辺を何倍かしただけでは係数がそろわないときは、それぞれ何倍かしてそろうようにします。 これは分数の通分と同じ考え方です。 この問題では (1)を4倍する と −12y ができ、 (2)を3倍する と 12y ができるので、足し算により y が消去でき3 なぜ掃き出し法で連立方程式の解が求まるのか？ 4 練習問題 41 解答連立方程式を解くには,xかyのどちらかの文字を１つ消去して,文字が1つだけの方程式にして解く。 この解き方に 加減法 と 代入法 がある。

高校数学で学習する連立方程式の解き方まとめ 数スタ

3分で分かる 二次方程式の問題の解き方をわかりやすく 合格サプリ

 今日はxの方程式の解き方の基礎的な手順を書いてみた。よかったら参考にしてみてね^^ 基礎編一次方程式の解き方の3つの手順 それでは簡単な1次方程式（xの方程式）の解き方を振り返ってみよう。xの方程式の具体例として、 7x2 = 5x 10 2 掃き出し法のやり方 21 ステップ1連立方程式を行列に変換する; 2次方程式 6xaxb=0 の二つの解が 1/3 と 2であるとき、 aとbのそれぞれの値を求めなさい。 Q方程式の問題を教えてください。 52(3X1)=4X3 方程式のやり方を忘れてしまいました(>_

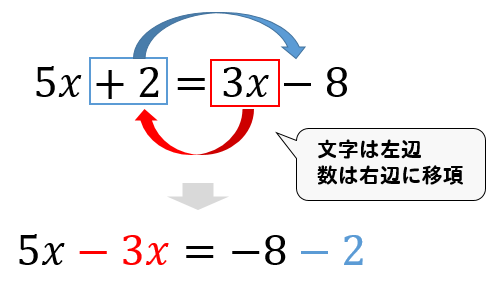
一次方程式の解き方を解説 かっこや分数の場合のやり方も 方程式の解き方まとめサイト

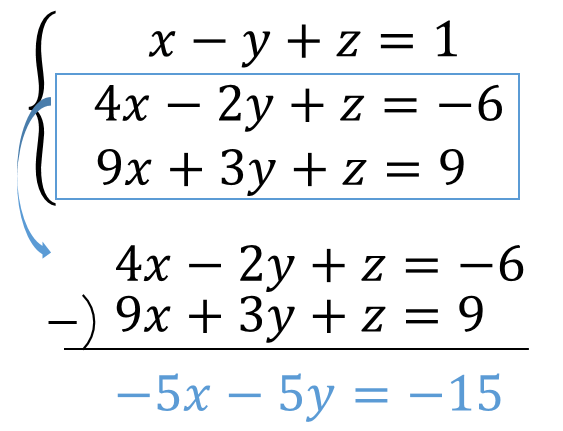
連立方程式 3つの文字 式の問題を計算する方法は 数スタ

 こういう方程式ってどうやって解けばいいんだろう？ ？ かず先生 因数分解を使った解き方 を利用するといいよ！ というわけで、今回の記事では二次方程式の解き方の1つ 「因数分解を使った解き方」 について解説していきます。 まぁ、簡単なやり方連立方程式の解き方は、下記の2つがあります。 加減法 ⇒ 1つの未知数が消えるように2つの方程式を加減し、もう一方の未知数の解を求める方法 代入法 ⇒ 1つの式を「x=」の形にして、もう一方の式に代入し解を求める方法 加減法、代入法の詳細は、下記 連立方程式には「 加減法 」「代入法」と2つの解き方があります。 この2つのうち、苦手としている人が多いのが今回取り上げる代入法を使った解き方です。

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点

中1方程式 分数が含まれるときの解き方を問題解説 Youtube

 線形代数連立方程式の解き方を徹底解説！ 逆行列の求め方やなぜ求まるのかを分かりやすく解説！ 連立方程式 行基本変形のやり方や掛け算での表し方を簡単に解移項のやり方、ルールと符号 移項のルールを下記に示します。 ・一方の辺の項を、別の項に移すとき符号を変える。「＋」⇒「－」、「－」⇒「＋」 ・方程式を解くときは、左辺に文字、右辺に数を移項する 下記を移項し未知数xの値を求めます。 x4 中学3年生で学習する二次方程式ですが とにかく解き方が多い！ 今回の記事では、これらの計算方法についてイチから解説をしていきます。 それぞれの練習問題も用意しているので この記事を通して二次方程式を完全マス

二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学

徹底解説 連立方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

★無料の中学メルマガ講座★毎週、問題と動画講義をお届け！ 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料 方程式と線分図の基本を説明してきました。 どちらのやり方が正しいとかではなく、自身に合った方法または、問題による使い分けで、やりやすい方で良いです。 ここでは、基本的例を挙げました。連立方程式でも線分図でも 『求められている答えは何か。中学生 12ヶ月前 めあ この問題の解説と、二元一次方程式のやり方を教えて下さい！ (この答えはウです) 二元一次方福式 2ェオキッリッ=6 の錠であるェエ、ヵの値の旨を の アからエまでの中から1つ選びなさい< PCE22GmにおSIの (③) 72計mm のey emi由

中学数学 一次方程式

この三元一次方程式の解き方を教えて下さい Clear

 このページは、こんな方へ向けて書いています 移項のやり方を教えてほしい なぜ符号が変わるのか知りたい 移項を使った計算のやり方を知りたい ここでは、方程式を解くために使う「移項」という操作について考えていきます。 まずは、移項のやり方についてを丁寧に解説していきます組立除法のやり方 上記の例題で述べた組立除法のやり方を整理します。 割られる多項式が三次式 f (x) = a 3 x 3 a 2 x 2 a 1 x a 0 f(x)=a_3x^3a_2x^2a_1xa_0 f (x) = a 3 x 3 a 2 x 2 a 1 x a 0 の場合を考えます。一般の n n n 次式の場合も全く同じです。 これから連立方程式を解く問題はこの行列の形で出題されますので、元の連立方程式がどういう形なのか分かるようにしておいてくださいね！ 連立方程式の解は3パターンある 連立方程式の解の出方は以下の3パターンです。 ・「 普通に解が出るパターン 」

連立方程式 1 代入法と加減法 バカでもわかる 中学数学

連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト

平方完成！文字を含む式の場合は？やり方を丁寧に解説！ 二次関数グラフの書き方を初めから解説！ 二次関数の式の作り方をパターン別に解説！ 二次関数を対称移動したときの式の求め方を解説！ 平行移動したものが2点を通る式を作る方法とは？★無料の中学メルマガ講座★毎週、問題と動画講義をお届け！ 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料方程式を、 2 x 4=10 から x =3 のように x = の形に変換することを、 方程式を解く と言います。ここでは一次方程式の解き方を解説していきます。 方程式の基本 方程式を解くに当たって基本となるのは、 移行・同類項の計算・左辺を文字のみにする の3つ

3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく

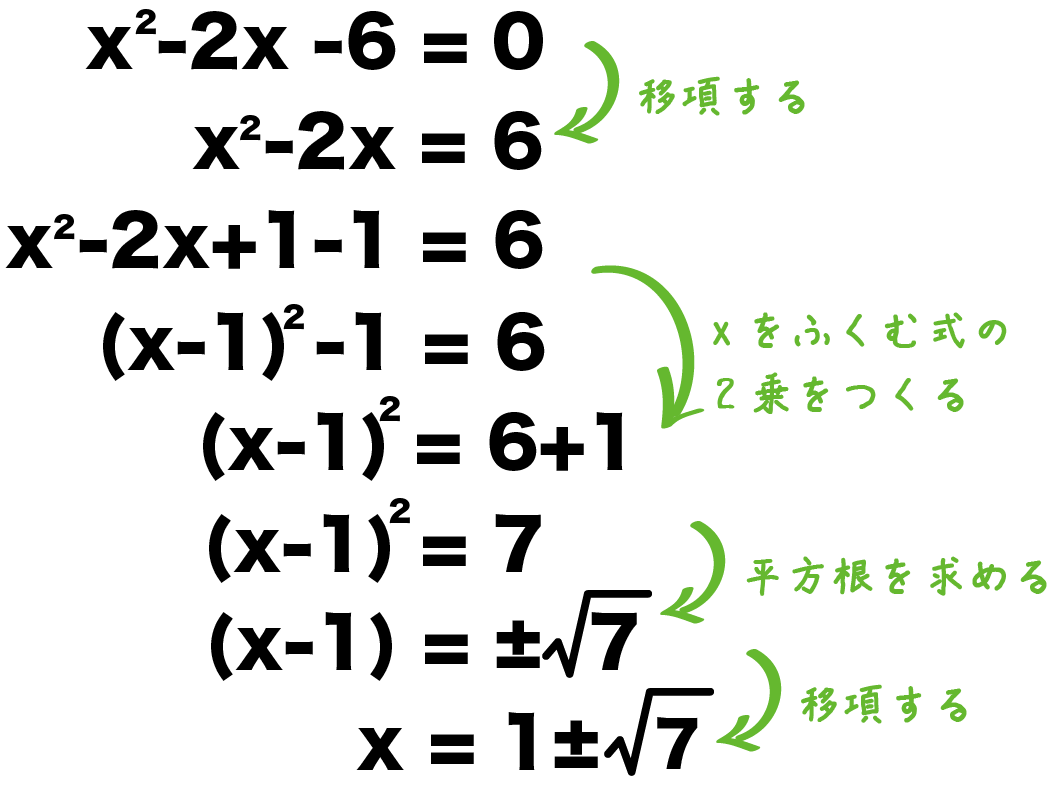
中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく

 わざわざ時間を使って、方程式とそうでない解き方の二通りのやり方を習うなんて、非効率的です。 まとめ 以上4点が、私が小学生の息子に方程式を教えない理由です。 子どもに方程式で解く方法を教えたいと思ったのは、誰のためでしょうか？ 10倍、100倍して小数を消せばいいよ！ というわけで、今回の記事では「小数を含む連立方程式の解き方」についてイチから解説していきます。 今回の記事では以下の問題の解き方について解説していくぞ！ 次の計算をしなさい。 ① ② ③ 方程式の基本1次方程式を解くとは 3x5=−1 (1) のように未知数 x を含む等式を x についての方程式といいます。 この頁では、1次方程式から「等式の性質」を使って解を求める方法を学びます。 x=··の形をした式を解といいます。

2

Q Tbn And9gcsudifqgece9d6jsq4 Iqqekos3ldkjmq4zbx6 Yyqy6wua7gy8 Usqp Cau

中3数学平方完成を用いた2次方程式のやり方(解き方)について解説します！ 中学生の勉強方法 214 中2数学多角形の内角の和と外角の和の求め方を解説！ 方程式に小数が含まれている場合 両辺を10倍、100倍して小数を消す！ 方程式に含まれる小数が、小数第1位までであれば両辺を10倍、小数第2位までであれば両辺を100倍します。 今回の方程式であれば、小数第1位までの小数なので両辺を10倍します。

一次方程式の問題や文章題の解き方を例題で詳しく解説 Studyplus スタディプラス

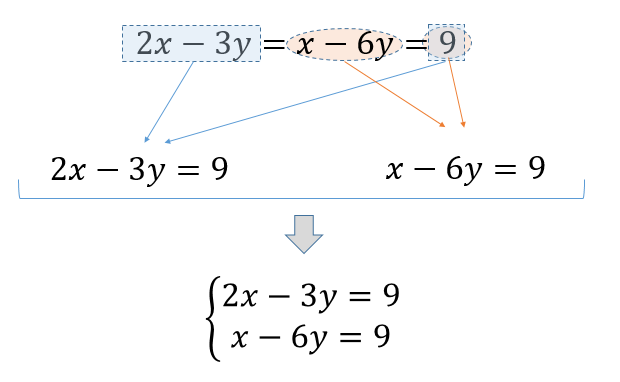
連立方程式３つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト

中1 数学 中1 29 方程式の解き方 編 Youtube

分数の方程式の解き方 分母を消せば中１の子でも絶対解ける 中学や高校の数学の計算問題

解き方 連立方程式の加減法がわかる4つのステップ Qikeru 学びを楽しくわかりやすく

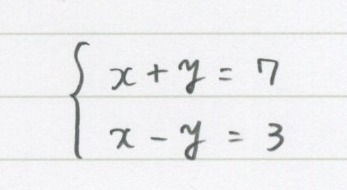
5 1 連立方程式 基本 勉強できようサイト

連立方程式の解き方と交点の座標の求め方 数学の偏差値を上げて合格を目指す

連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料

数学 中2 19 ややこしい連立方程式 Youtube

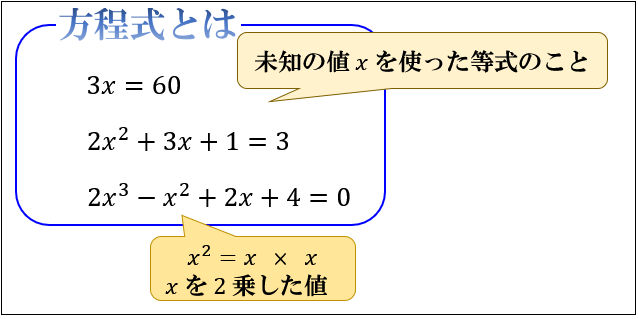
二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ

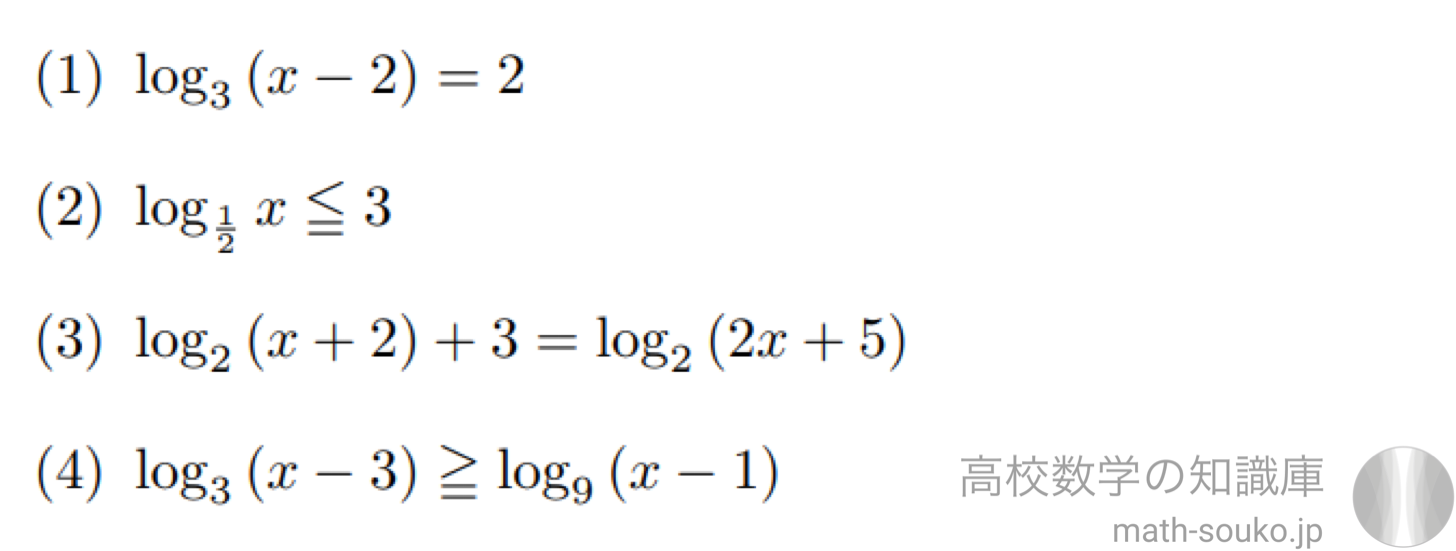
対数方程式と対数不等式の解き方 高校数学の知識庫

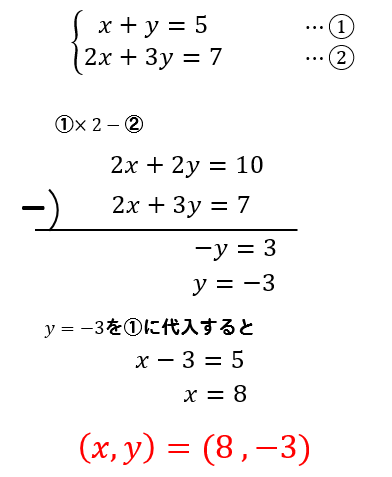
方程式練習問題 連立方程式 A B C 方程式の解き方まとめサイト

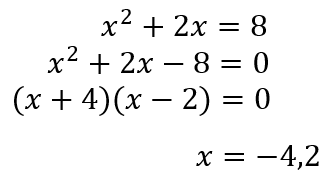
アルジャブル 昔のかしこな人の二次方程式 キソカラ

お勉強 連立方程式の解き方のご提案 去年の男子女子ｘ ｙ人の問題 そらの暇つぶしch

中２連立方程式の解き方と計算問題 代入法と加減法 Irohabook

中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点

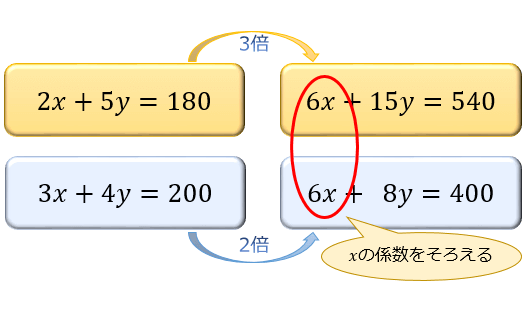
連立方程式 加減法 の解き方 なぜ加減法が成り立つか アタリマエ

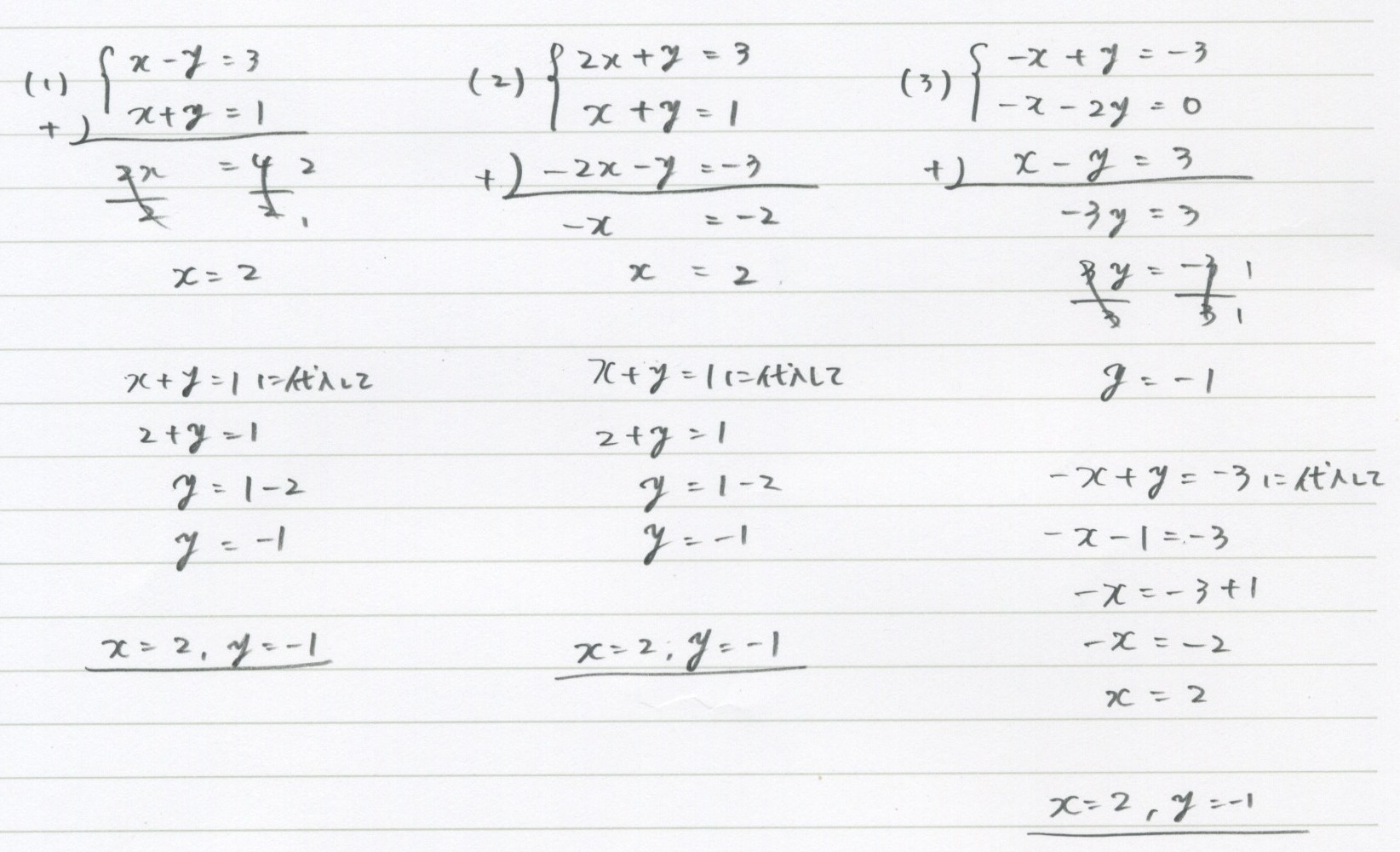
5 1 連立方程式 基本 勉強できようサイト

連立方程式の利用の問題の解き方 年齢の問題 1 現役塾講師のわかりやすい中学数学の解き方

連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト

二次方程式の解の公式 因数分解による解き方を解説 解の公式をマスター Studyplus スタディプラス

中１ 数学 中1 30 方程式を解く 小数と分数編 Youtube

連立方程式の2つの解き方 代入法 加減法 数学fun

連立方程式を小学生に教える

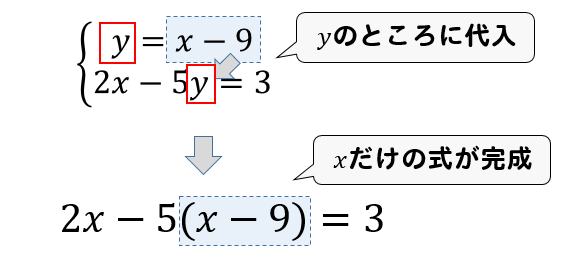
連立方程式 代入法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト

高校数学 ３次方程式 解き方一覧 因数分解 置換 組立除法 学校よりわかりやすいサイト

１次方程式 小数 分数をふくむ1次方程式の解き方 中学数学 定期テスト対策サイト

2次方程式 2 どの方法で解けばいいの バカでもわかる 中学数学

中１ １次方程式 でつまずく原因と解決法 分数

中1数学 方程式の解き方４ カッコ 分数 小数 例題編 映像授業のtry It トライイット

分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題

連立方程式の解き方 加減法 Youtube

一次方程式の解の求め方 数学fun

2次方程式 1 解き方 因数分解 平方根 平方完成 解の公式 バカでもわかる 中学数学

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

第１章 連立方程式

方程式

数学 方程式の解き方をわかりやすくまとめました 簡単に解くための たった２つポイントとは 中１ 方程式 中学数学 数学 行間 ぎょうのあいだ 先生

３次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ

連立方程式の解き方 Youtube

2次方程式とは 1分でわかる意味 解き方 解の公式 因数分解との関係

3

１次方程式の解き方 １ 無料で使える中学学習プリント

数学の連立方程式のやり方が分かりません 教えてくれると有難いです Clear

二次方程式の解き方のまとめ 中学生に覚えてほしいパターンは５つ 中学や高校の数学の計算問題

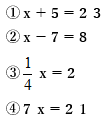
方程式の解き方をマスターしよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

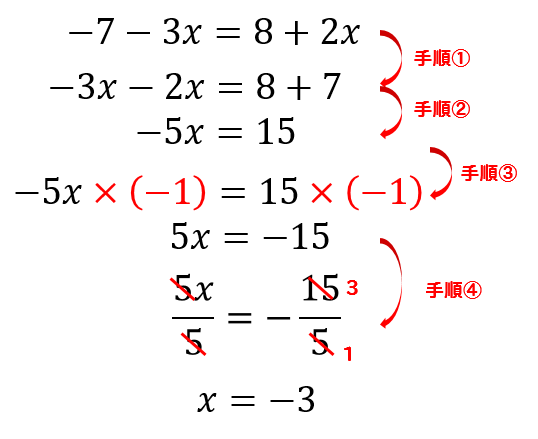
中１方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ

数学 中2 15 連立方程式 加減法の基本編 Youtube

大まかな解き方だけで 途中式はなくても良いのでこの連立方程式のやり方教えて下さい Clear

高次方程式とは 因数分解 因数定理による解き方と計算のコツ 受験辞典

不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典

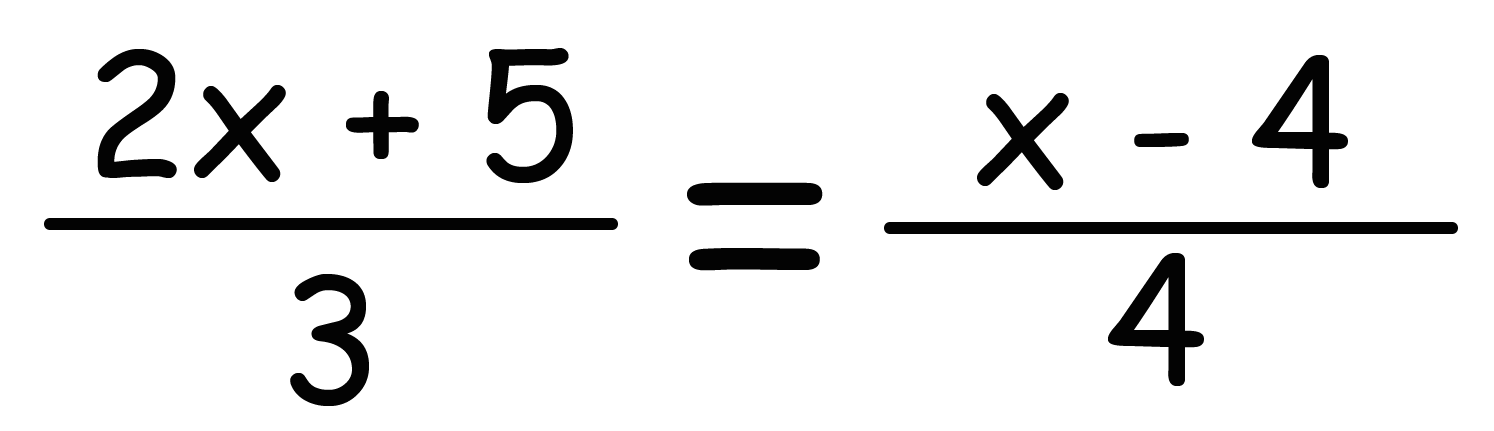
中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく

勉強しよう数学 ２次方程式の解き方 解の公式を使わず以下の様に解く

連立方程式の解き方 加減法 代入法と文章題の計算方法 リョースケ大学

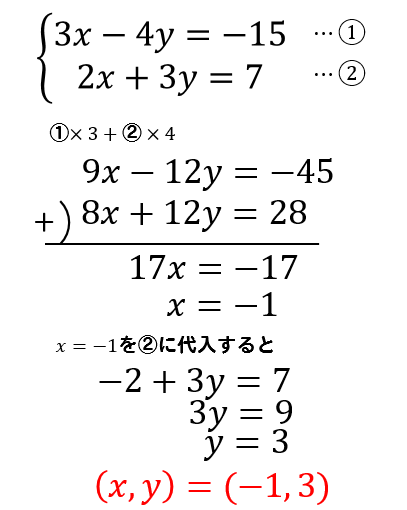
連立方程式 加減法の解き方をわかりやすく問題を使って徹底解説 数スタ

連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料

数学の高次方程式問題 解き方のコツ 公式 スタディサプリ大学受験講座

小数の連立方程式の解き方 両辺を１０倍や１００倍しよう 中学や高校の数学の計算問題

一次方程式とは 慶應生が解き方3ステップ教えます 問題 文章題付き 高校生向け受験応援メディア 受験のミカタ

スタディピア 1次方程式

方程式の種類と解き方 中学で学習する方程式ってどんなのがある 中学数学 理科の学習まとめサイト

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者

中2 数学 連立方程式の解き方二通りを解説 授業動画あり アオイのホームルーム

中学数学 二次方程式の解き方はこの3パターンだけでok 平方根 因数分解 解の公式 楽スタ

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

二次方程式の解き方をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学

中学校数学 3年生 数量 2次方程式 Wikibooks

中学生連立方程式の解き方を教えてください この答えにはどうやってた Yahoo 知恵袋

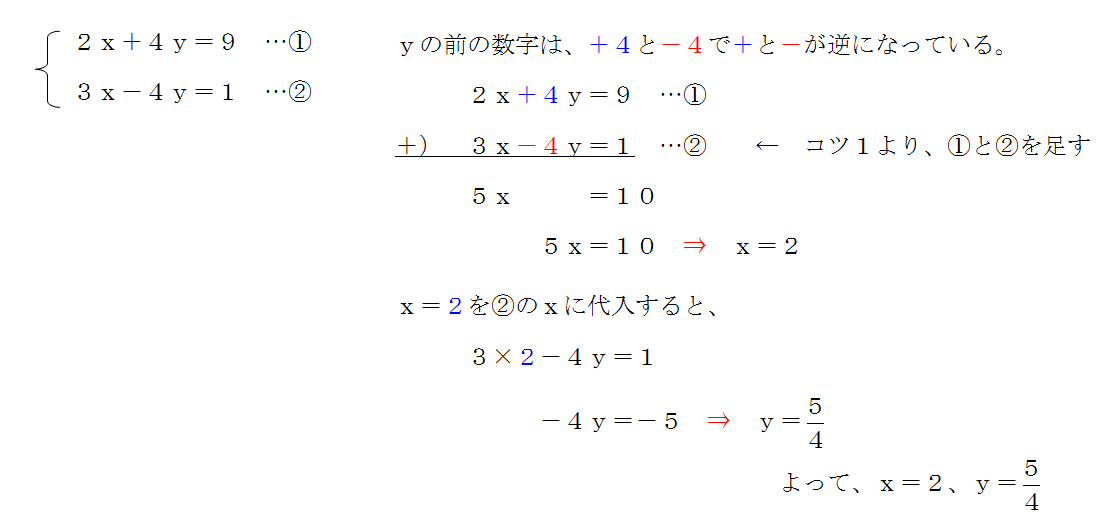
連立方程式の解き方 問題の文字を消すことが解き方のコツだ 三重の個人契約家庭教師

勉強しよう数学 ２次方程式の解き方 解の公式を使わず以下の様に解く

第１章 連立方程式

48s96ub7b0z5f Net Taisuu Houteishiki

1

方程式の解き方 簡単な問題で 解き方のコツを覚えよう 中学や高校の数学の計算問題

中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット

基礎数学演習ｉ

方程式とは 1分でわかる意味 移項 １次方程式の解き方と計算問題 分数の関係

中3 中3数学 2次方程式 中学生 数学のノート Clear

中1 数学 中1 28 方程式の解き方 基本編 Youtube

Studydoctor連立方程式の解き方 加減法 中２数学 Studydoctor

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

Q Tbn And9gcrajuxoiaqucb6pp9lfayav 0a2hxopnjg8ig Xj1i4ot74xb6j Usqp Cau

連立方程式の加減法の解き方をマスターしたい方は見てください 中学や高校の数学の計算問題

Studydoctorかっこのついた連立方程式 中２数学 Studydoctor

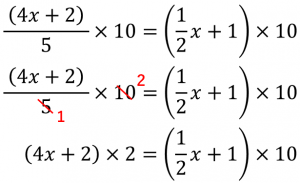
中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす

中学1年数学 一次方程式 一次方程式の解き方 移項の本当の意味を理解すれば全部解ける 数学の面白いこと 役に立つことをまとめたサイト